我們昨天講了以下的密碼協議：

今天我們來研究為什麼他是個晶格密碼系統，並把它破掉！

回顧正確性證明

我們在做解碼的時候，其實用到了幾件事：
第一點：在私鑰裡面， h = f^(-1) * g mod q
第二點：f, g, m, r 都不太大，具體來說是滿足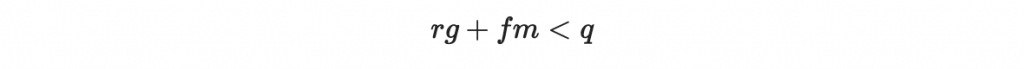

第三點：m 比 g 還要小，滿足 m < g

所以根據第一點與第二點，我們在模除 q 的環中計算 a = fe 其實得到整數上的相等：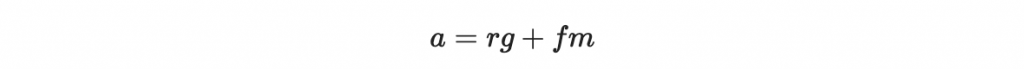

再根據第三點，我們在模除 g 的環中計算 b = f^(-1) * a 其實得到整數上的相等：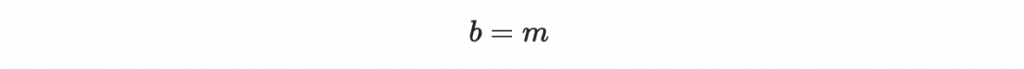

於是解碼成功。

現在，攻擊者如果想要正確得到明文 m ，他需要生成一把偽造鑰匙 (F, G) 滿足以上三點，於是可以解碼。也就是說
第一點：h = F^(-1) * G mod q
第二點：F, G, m, r 都不太大，滿足

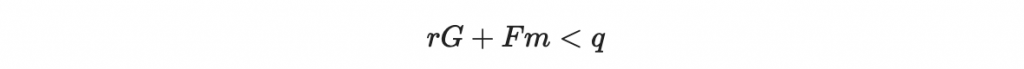
第三點：m 比 G 還要小，滿足 m < G

可是我們細一點看，第二點其實很難做到，因為我必須先知道 r 與 m ，我才可以計算 rG+Fm ，並看看有沒有小於 q 。啊，我如果知道 r 跟 m，那我就知道 m 啦，做完了。

因此，我們能做的目標，其實只是「希望 F 與 G 儘量的小」。

另外，第三點的部分指出： m < G 才能解碼成功，不過其實如果第二點滿足了，而第三點沒有滿足，頂多是 b 與 m 差了整數倍，我們已經消掉了許多的可能，所以關鍵其實是在第二點！

總結此段：為了還原明文 m ，我們希望找到儘量小的 (F, G) 使得

晶格

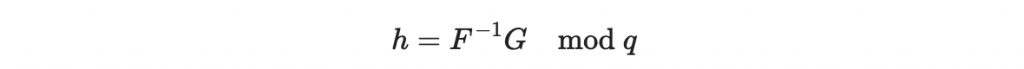
為了還原明文 m ，我們希望找到儘量小的 (F, G) 使得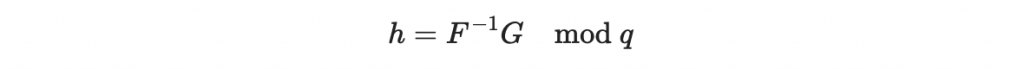

我們把這個算式改寫成：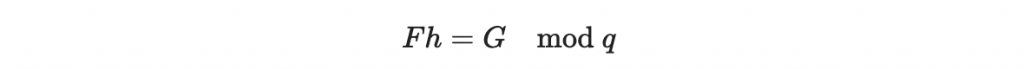

把他們拉回整數環，得到：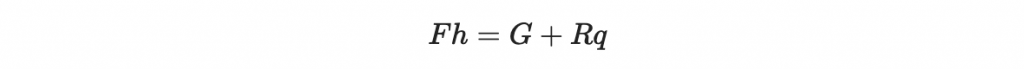

其中 R 是個整數，最後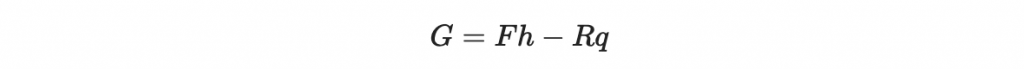

然後因為我們希望 (F, G) 儘量小，所以我們可以把 (F, G) 當成向量，寫成線性組合，然後希望 (F, G) 儘量小：

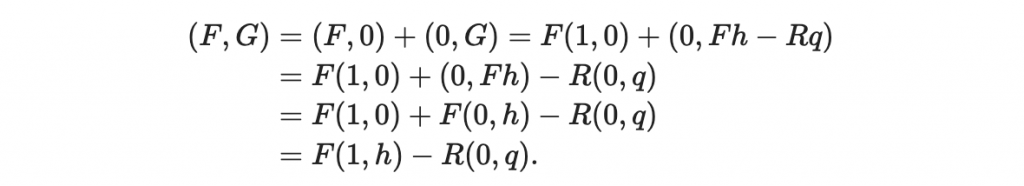
因此我們寫出：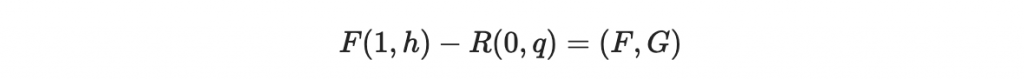

然後我們的目標是希望 (F, G) 越小越好。

翻譯一下喔。意思是，我們要找到向量 (1, h) 以及 (0,q) 的整係數線性組合，好讓結果 (F, G) 越小越好。是不是有晶格密碼學的味道了😀

破密學

好，相信你已經接受以上的密碼系統是晶格密碼學了，而且晶格密碼學是後量子密碼學主流作法之一，他應該超難破的吧？

很不幸的，上面這個已經被高斯破了。（算是某種發論文然後穿越時空的破密法）😂 這個演算法就叫做 Gauss Reduction 。中文應譯做高斯化約，請不要和高斯消去搞混。

其實概念很簡單，大家花一個晚上想想也知道這個怎麼破。就是你現在有兩個向量

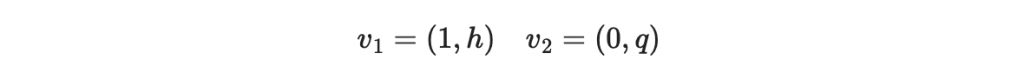
然後你把比較長的那個，扣掉比較短的那個的整數倍，使得兩個向量可以「接近垂直一點」。這樣的過程做好幾次後，你就會得到兩個很接近垂直，而且不會太長的向量（因為你過程中一直做減法，中間總會有幾步的結果是短一點的。

好，我們用 SageMath 來破密。回顧上一次出現的參數：

公鑰 q = 1408922792
公鑰 h = 466771449
私鑰 f = 1473
私鑰 g = 21881
（我們不用用到 f 和 g）

密文 e = 1080936575
明文 m = 15819

q = 1408922792
h = 466771449
e = 1080936575
mess = 15819

並且宣告兩個向量：

v1 = vector([0,q])
v2 = vector([1,h])

print(v1,v2)


Outputs:   
(0, 1408922792) (1, 466771449)

我們可以透過計算 dot product 來得到兩個向量的長度關係：

print(v1.dot_product(v1) , v2.dot_product(v2))

print(v1.dot_product(v1) >= v2.dot_product(v2))


Outputs:   
1985063433817075264 217875585601559602 
True

因此 v1 是比 v2 要長。現在，我們希望把 v1 扣掉整數倍的 v2 ，好得到兩個比較接近垂直的向量：

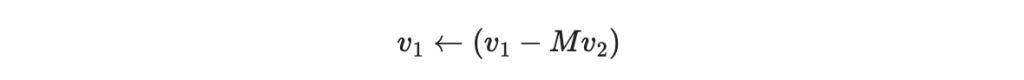
因為我們希望儘量垂直，所以我們希望以下內積要盡可能等於零：

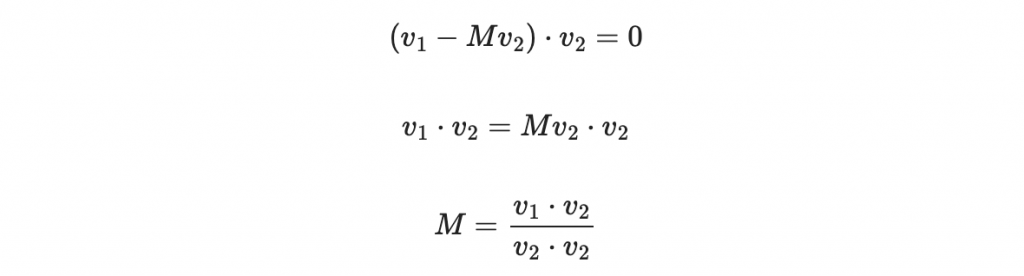
然而 m 是整數，所以我們只能退而求其次，取以上算式的四捨五入：

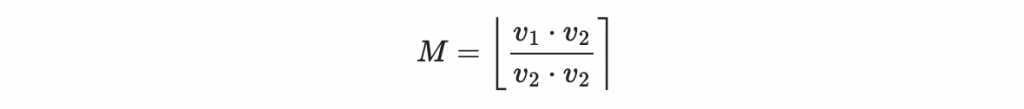
其中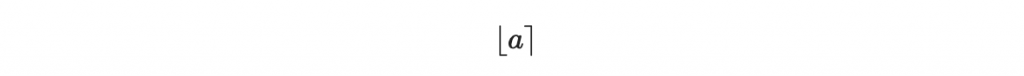

指的是 a 的四捨五入。

我們使用 SageMath 來完成這個動作：

print(v1,v2)
M = round(((v1.dot_product(v2))/(v2.dot_product(v2))))
print(v1, v1 - M*v2)

Outputs: 
(0, 1408922792) (1, 466771449)
(0, 1408922792) (-3, 8608445)

姑且不看新的向量有沒有更加垂直，從數字上就可以看出，我們已經找到一個相對短的向量 (-3, 8608445) 了。

這樣的過程可以做很多遍，直到 m 只能四捨五入到零為止。此時，我們就得到一組新的 v1, v2 ，相當小，而且仍然能生成原本所有可能的 (F,G) ：

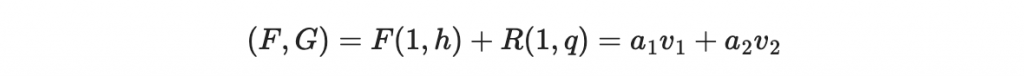
通常來說，最後取一個 a_1 = 1, a_2 =0 ， (F, G) = v1 就可以拿去解碼了。

我們定義一個函數如下，函數的語法可以從 python 照搬

def Gauss_reduction(v1,v2):
    while True:
        if v2.norm() < v1.norm():
            temp = v2
            v2 = v1
            v1 = temp
        
        M = round(((v1.dot_product(v2))/(v1.dot_product(v1))))

        print("v1 =", v1, "v2 =", v2)
        if M == 0:
            return (v1,v2)
        
        
        v2 = v2 - M*v1

輸出結果：

v1_red, v2_red = Gauss_reduction(v1,v2)
print("\n"+"v1_red =", v1_red, "v2_red =", v2_red)

Outputs:
v1 = (1, 466771449) v2 = (0, 1408922792)
v1 = (-3, 8608445) v2 = (1, 466771449)
v1 = (163, 1915419) v2 = (-3, 8608445)
v1 = (-655, 946769) v2 = (163, 1915419)
v1 = (1473, 21881) v2 = (-655, 946769)
v1 = (1473, 21881) v2 = (-63994, 5886)

v1_red = (1473, 21881) v2_red = (-63994, 5886)

好，現在我們把 (F, G) = (1473, 21881) ，並做以下的標準解碼動作：

第一步：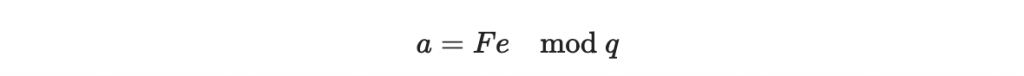

第二步：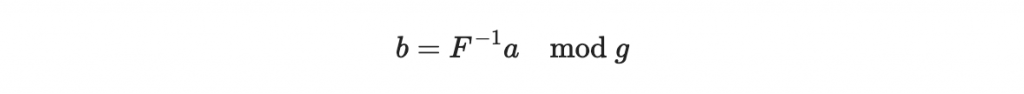

使用 SageMath 來計算：

F,G = 1473, 21881

第一步：

R_q = quotient(ZZ, q*ZZ)
F = R_q(F)
e = R_q(e)

a = F*e
print(a)

Outputs: 136820015

第二步：

R_G = quotient(ZZ,G*ZZ)
a = R_G(a.lift())
F = R_G(F.lift())

b = F^(-1)*a
print("b = " ,b)
print("m = " ,m)

Outputs:
b = 15819 
m = 15819

恭喜，破密成功

Takeaway

• 為什麼昨天的密碼系統可以說是晶格密碼系統？因為我們可以透過重新找到相對小的 (F, G) 滿足 h = F^(-1) G ，並把這樣的 (F,G) 當做密鑰來使用
• 這樣的密碼系統並不安全，因為我們可以透過 Gauss Reduction 來找到相對小的 (F, G) 。

ref:

SILVERMAN, Joseph H.; PIPHER, Jill; HOFFSTEIN, Jeffrey. An introduction to mathematical cryptography. Springer New York, 2008.